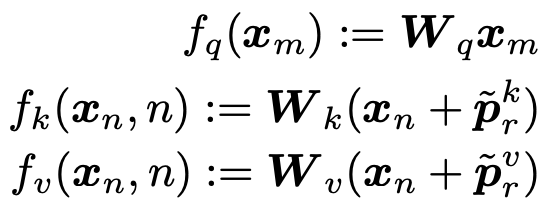正在更新中……
秋招在即,用这篇博客记录一下算法岗求职过程中的一些必备知识汇总。
激活函数
激活函数作用
如果不用激活函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合,这种情况就是最原始的感知机(Perceptron)。使用激活函数能够给神经元引入非线性因素,使得神经网络可以任意逼近任何非线性函数,使深层神经网络表达能力更加强大,这样神经网络就可以应用到众多的非线性模型中
激活函数分类

常见激活函数
Sigmoid
数学表达式:;
导数表达式:;
函数图像:缺点:容易造成梯度消失;消耗计算资源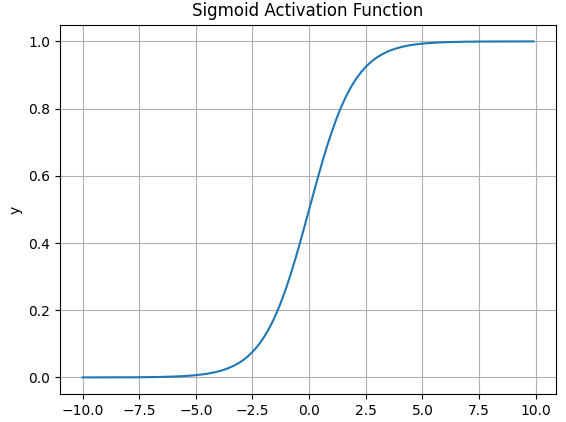
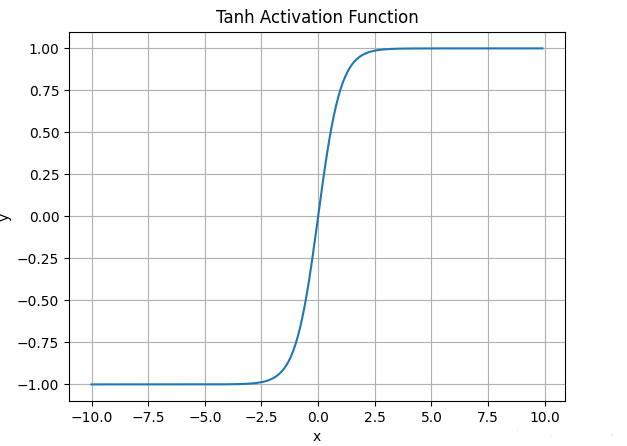
Tanh
数学表达式:;
函数图像:缺点:与Sigmoid类似
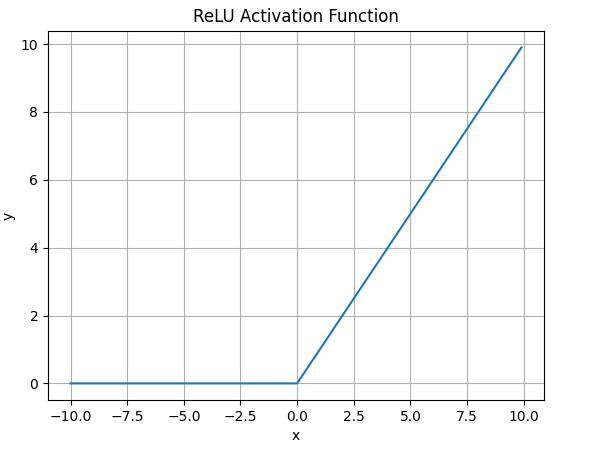
ReLU
数学表达式:;
函数图像:优点:相较于上面的改进:解决了梯度消失,当输入为正时,不会饱和;由于ReLU线性非饱和的性质,在SGD中能快速收敛;计算复杂度低。 缺点:与Sigmoid一样不是以0为中心的;Dead ReLU,当输入为负时,梯度为0。这个神经元及之后的神经元梯度永远为0,不再对任何数据有所响应,导致相应参数永远不会被更新。
PReLU
数学表达式:,其中xi代表的是第i个通道的输入,这里允许不同通道的激活函数不一样。ai是一个自适应可学习的参数。当a=0时退化为ReLU;当a固定时,退化为LeakyReLU。
优点:a可以自适应学习,从而获得每个通道专门的激活函数。
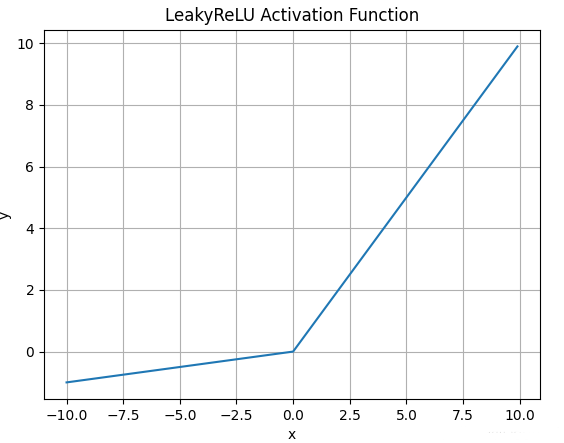
LeakyReLU
数学表达式:;
函数图像:优点:解决了Dead ReLu问题;线性非饱和;计算复杂度低。 缺点:a需要先验知识人工赋值。
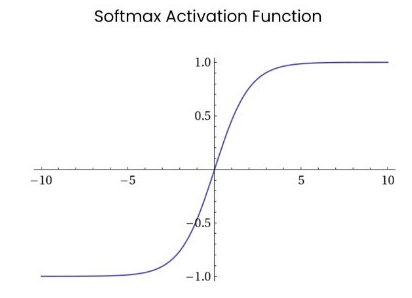
Softmax
数学表达式:;
函数图像:Softmax函数常在神经网络输出层充当激活函数,将输出层的值通过激活函数映射到0-1区间,将神经元输出构造成概率分布,用于多分类问题中,Softmax激活函数映射值越大,则真实类别可能性越大。
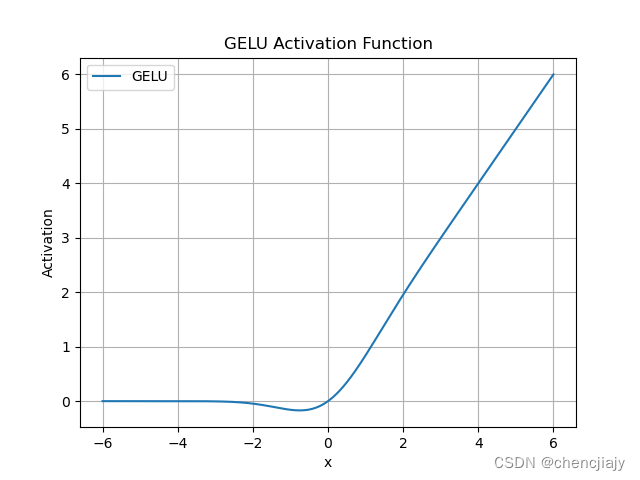
GELU
数学表达式:,其中P(X<=x)是高斯分布,一般取标准分布。
函数图像:
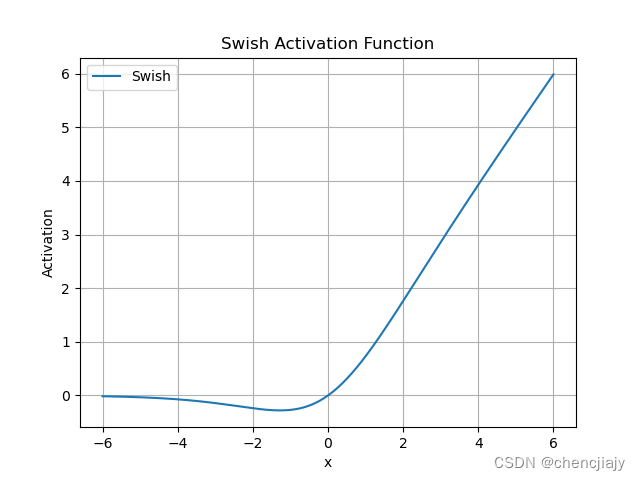
Swish
数学表达式:,是sigmoid函数。是超参数。当是1时,就是SiLU激活函数。
函数图像:
GLU(Gated Linear Unit)
数学表达式: , 是矩阵的按元素乘, W,V,b,c为可学习参数。
SwiGLU
数学表达式:,将GLU中的sigmoid换成了Swish。相对于ReLU的优势:
- 平滑的转换:SwiGLU在0附近提供了更平滑的转换,这有助于更好的优化过程。
- 门控特性:SwiGLU继承了GLU的门控机制,可以根据输入情况决定哪些信息应该通过,哪些应该被过滤,这有助于提高模型的泛化能力,特别是在处理长序列、长距离依赖的文本时。
- 可学习参数:SwiGLU中的参数可以通过训练学习,使得模型可以根据不同任务和数据集动态调整这些参数,增强了模型的灵活性和适应性。
- 非线性能力:SwiGLU相比于ReLU,在负值区域也有响应,这克服了ReLU在负输入下输出始终为零的缺点,使得网络可以更有效地学习到有用的表示。(DeadReLU,有助于缓解梯度消失)
SwiGLU代码:
1 | import torch |
RNN/GRU/LSTM
Transformer
Encoder,Decoder
Transformer结构描述
见下图
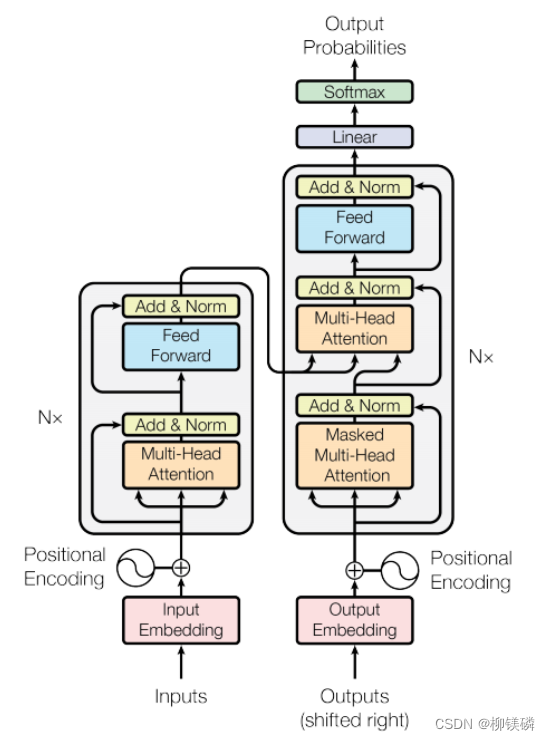
简述Transformer中的FFN。
使用了ReLU作为激活函数。
Decoder和Encoder是如何进行交互的?
Cross attention。Decoder提供Q,Encoder提供K,V。
Decoder和Encoder结构的差别
Encoder的MHSA中需要对padding部分进行mask;Decoder部分的第一个MHSA是self-attention,并且这部分需要引入casual mask避免后面的序列看到前面的序列;Decoder部分的第二个MHA是Cross-attention,其中Q来自前一部分的输出,K,V来自Encoder的输出。
Decoder在进行推理时的解码策略?
- Random Sampling:按照概率分布随机选择一个单词。这种方法可以增加生成的多样性,但是可能会导致生成的文本不连贯和无意义.
- Greedy Search:直接选择概率最高的单词。这种方法简单高效,但是可能会导致生成的文本过于单调和重复。
- Beam Search:维护一个大小为 k 的候选序列集合,每一步从每个候选序列的概率分布中选择概率最高的 k 个单词,然后保留总概率最高的 k 个候选序列。这种方法可以平衡生成的质量和多样性,但是可能会导致生成的文本过于保守和不自然。
- Top-k sampling:是对贪心策略的优化,它从排名前 k 的 token 中进行抽样,允许其他分数或概率较高的token 也有机会被选中。在很多情况下,这种抽样带来的随机性有助于提高生成质量。在每一步,只从概率最高的 k 个单词中进行随机采样,而不考虑其他低概率的单词。
- Top-p sampling(也叫Nucleus sampling):在每一步,只从累积概率超过某个阈值 p 的最小单词集合中进行随机采样,而不考虑其他低概率的单词。这种方法也被称为核采样(nucleus sampling),因为它只关注概率分布的核心部分,而忽略了尾部部分。
手撕简易版Beam Search
1
残差的作用
与Resnet相同,解决梯度消失,防止过拟合,加速模型收敛。
Transformer是如何做到并行的?
在Encoder的并行化主要体现在Self-attention模块,可以并行处理整个序列,并得到整个输入序列经过Encoder端的输出,但RNN只能从前到后的串行执行。
在Decoder端,训练的时候使用Teacher-forcing训练方式,因此也可以并行;但推理的时候仍然是自回归的模式。RNN,CNN和Transformer的区别
RNN(递归神经网络):
时间序列处理:RNN特别适用于处理序列数据,如时间序列、自然语言等。
递归结构:RNN通过递归地应用相同的权重来处理序列中的每个元素,允许信息在序列中流动。
参数共享:在序列的每个时间步上,RNN使用相同的权重矩阵。
问题:RNN在处理长序列时可能会遇到梯度消失或梯度爆炸的问题,这限制了它们学习长期依赖关系的能力。
CNN(卷积神经网络):
空间特征提取:CNN主要用于图像处理,通过卷积层提取图像的空间特征。
局部连接:每个卷积神经元只与输入数据的一个局部区域相连接,这减少了参数的数量。
参数共享:卷积核在整个输入数据上滑动,共享相同的权重。
层次结构:CNN通常具有多个卷积层,每个层级可以捕捉不同级别的特征。
应用:CNN在图像分类、目标检测和图像分割等领域非常成功。
Transformer:
自注意力机制:Transformer使用自注意力机制来处理序列数据,允许模型在编码每个元素时考虑到序列中的所有其他元素。
并行处理:由于自注意力机制,Transformer可以并行处理序列中的所有元素,这大大提高了训练效率。
无循环结构:与RNN不同,Transformer没有递归或循环结构,这使得它们在处理长序列时更加有效。
多头注意力:Transformer通常使用多头注意力,这允许模型同时学习序列数据的多个表示。
应用:Transformer在自然语言处理任务中非常流行,如机器翻译、文本摘要和问答系统。
总结来说,RNN适合处理序列数据,但可能在长序列上遇到训练问题;CNN擅长提取图像的空间特征,但在处理序列数据时可能不是最佳选择;而Transformer通过自注意力机制有效地处理序列数据,且能够并行处理,使其在自然语言处理任务中非常有效。每种架构都有其优势和局限性,选择哪一种取决于具体的应用场景和数据类型
Attention
- Attention机制描述
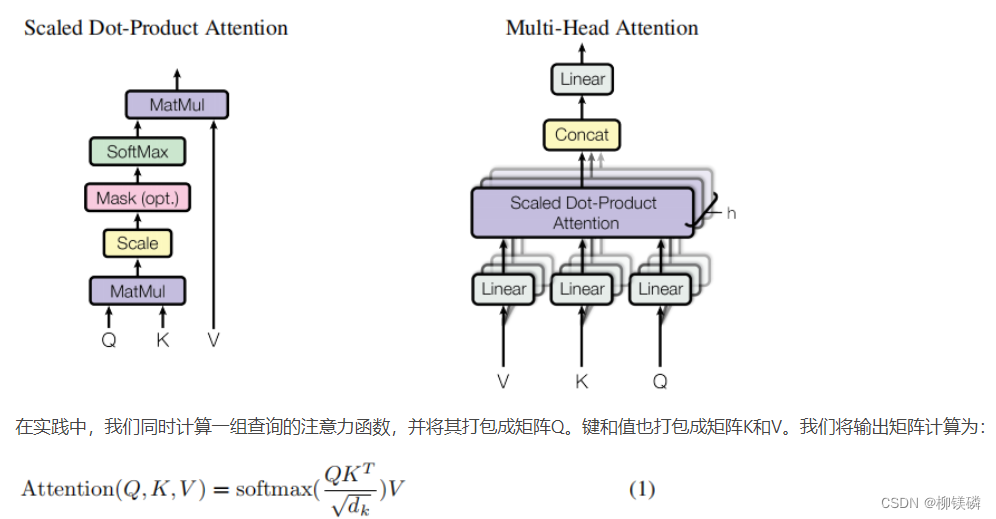
- Attention的复杂度
单头注意力的计算复杂度:
假设输入序列长度为,输出序列长度为,词向量的维度为。计算复杂度约为。
多头注意力的计算复杂度:
假设输入序列长度为,输出序列长度为,词向量的维度为,有,每个头的维度为。计算复杂度约为。
尽管Multi-head attention引入了多个头,但由于每个头的维度减小,并且计算可以并行进行,其总计算复杂度与单头Attention相同,即O(L⋅M⋅d)。然而,实际应用中,由于并行计算和维度分割,Multi-head attention通常能够更有效地利用计算资源。
Attention中为什么除以sqrt(k)?
在计算时,假设Q和K的维度为,其中每个元素期望值是0,方差为1,,这使得的期望为0,方差为。因此,在计算softmax时,如果比较大,的值也会很大,导致softmax输出非常尖锐的分布,会出现指数溢出或梯度消失的问题,难以训练。因此对进行缩放,是的每个元素的方差变为1,避免了上述问题。
综上,提升了模型的训练效果和稳定性在计算Attention score时,如何对Padding做mask?
一般有两种方式:
- Padding mask:将填充位置对应的token设置为一个很大的负数(如负无穷),这样在进行softmax计算式,填充位置对应的权重就会趋近于0,这样计算注意力时就不会考虑填充位置的信息。
- Masked softmax: 在softmax之前,将填充位置对应的token的score设置为一个很小的值,然后再进行softmax。
为什么要用Multi-head Attention?
- 并行计算: 多头注意力机制允许模型同时关注输入序列的不同部分,每个注意力头可以独立计算,从而实现更高效的并行计算。这样能够加快模型的训练速度。
- 提升表征能力: 通过引入多个注意力头,模型可以学习到不同类型的注意力权重,从而捕捉输入序列中不同层次、不同方面的语义信息。这有助于提升模型对输入序列的表征能力。
- 降低过拟合风险:多头注意力机制使得模型可以综合不同角度的信息,从而提高泛化能力,降低过拟合的风险。
- 降低计算复杂度: 通过对每个头进行降维,使得每个头的参数量减少,进而降低计算复杂度。
- 手搓Multi-head attention
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52import torch
import torch.nn as nn
import torch.nn.functional as F
class MultiHeadAttention(nn.Module):
def __init__(self, heads, d_model):
super().__init__()
self.d_model = d_model
self.d_k = d_model // heads # 每个“头”对应的维度
self.h = heads # “头”的数量
# 初始化线性层,用于生成Q,K,V
self.q_linear = nn.Linear(d_model, d_model)
self.k_linear = nn.Linear(d_model, d_model)
self.v_linear = nn.Linear(d_model, d_model)
# 输出线性层
self.out = nn.Linear(d_model, d_model)
def attention(self, q, k, v, mask=None):
# q,k,v [...,d]
# 计算点积,并通过 sqrt(d_k) 进行缩放
scores = torch.matmul(q, k.transpose(-2, -1)) / math.sqrt(self.d_k)
# 如果有 mask,应用于 scores
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9)
# 对 scores 应用 softmax
scores = F.softmax(scores, dim=-1)
# 获取输出
output = torch.matmul(scores, v)
return output
def forward(self, q, k, v, mask=None):
# q,k,v:[B,T,d]
batch_size = q.size(0)
# 对 q,k,v 进行线性变换
q = self.q_linear(q).view(batch_size, -1, self.h, self.d_k).transpose(1, 2)
k = self.k_linear(k).view(batch_size, -1, self.h, self.d_k).transpose(1, 2)
v = self.v_linear(v).view(batch_size, -1, self.h, self.d_k).transpose(1, 2)
# 进行多头注意力计算
scores = self.attention(q, k, v, mask)
# 将多个头的输出拼接回单个张量
concat = scores.transpose(1, 2).contiguous().view(batch_size, -1, self.d_model)
# 通过输出线性层
output = self.out(concat)
return output
Positional Encoding
Positional Encoding的作用
因为self-attention是位置无关的,无论句子的顺序是什么样的,通过self-attention计算的token的hidden embedding都是一样的,这显然不符合人类的思维。因此要有一个办法能够在模型中表达出一个token的位置信息,transformer使用了固定的positional encoding来表示token在句子中的绝对位置信息。
Transformer使用的位置编码
Sinusoidal Positional Encoding。这是一种绝对位置编码。的内积会随着相对位置的递增而减小,从而表征位置的相对距离,但由于距离的对称性,此方法虽然能够反应相对位置的距离,但是无法区分方向,即。见下图
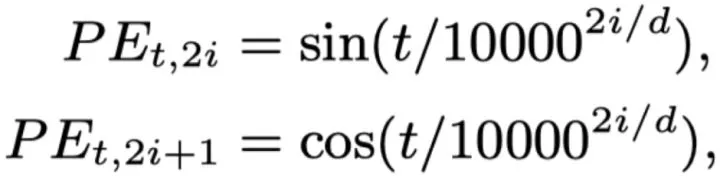
什么是大模型的外推性?
外推性是指大模型在训练时和预测时的输入长度不一致,导致模型的泛化能力下降的问题。
不同种Positional Encoding
此处参考苏神的文章
绝对位置编码:- Learnable Positional Encoding:直接将位置编码当作可训练参数。BERT,GPT,ALBERT等模型用的就是这种。缺点是没有外推性,无法感知相对位置。
- Sinusidal Positional Encoding:虽然pos+k可以被pos线性表示,这提供了表达相对位置信息的可能性,但不能表示方向。还具有远程衰减的性质。没有外推性。
- Autoregressive:RNN就属于这种,它本身自带位置信息。
相对位置编码:相对位置并没有完整建模每个输入的位置信息,而是在算Attention的时候考虑当前位置与被Attention的位置的相对距离。这一部分需要继续学习《Self-attention with Relative Position Representation》等文章。
- 显式的相对位置(Self-attention with Relative Position Representation):对于第m和第n个位置的token,其相对位置可以表示为,即两个token之间的相对距离。因此,相比于绝对位置,相对位置只需要有个表征向量即可,即在计算两个token之间的attetnion score时,只需要在attention中注入相对位置表征向量即可。这样可以表征任意长度的句子:
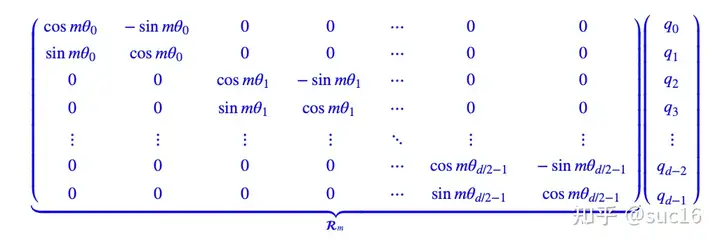
旋转位置编码(RoPE):通过绝对位置编码的方式实现了相对位置编码,对attention中的q、k向量注入了绝对位置信息,qk内积就会引入相对位置信息。(具体推导见苏神论文)见下图:
这里的\theta采取的和Transformer中一致,可以带来远程衰减的性质。
- 手撕Sinusoidal PE
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class PositionalEncoding(nn.Module):
def __init__(self, d_model, max_len=5000):
super(PositionalEncoding, self).__init__()
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
pe = pe.unsqueeze(0).transpose(0, 1)
#pe.requires_grad = False
self.register_buffer('pe', pe)
def forward(self, x):
return x + self.pe[:x.size(0), :]
BatchNorm,LayerNorm,Dropout,etc
- BatchNorm原理
训练时前向传导见下图:
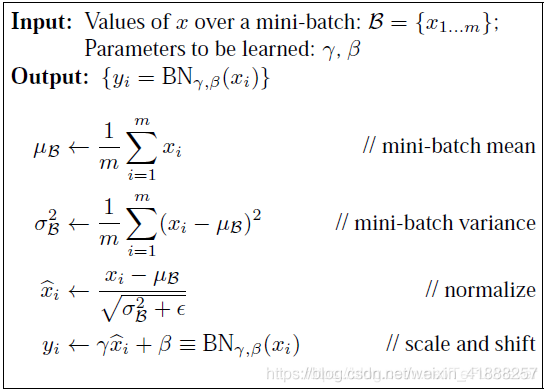
包含可学习参数,让网络可以学习恢复出原始数据的特征分布。同时也保存整个训练集的,使用移动平均法更新。
BatchNorm的优劣
优点:解决内部协变量偏移,加速模型收敛;增强模型稳定性,允许使用更高的学习率,提高模型泛化能力。
缺点:对batch size敏感(batch size较小时效果差,可用Group Normalization代替);不适用于变长序列;在推理阶段额外计算。BatchNorm训练和推理时的区别
我们在预测阶段,有可能只需要预测一个样本或很少的样本,没有像训练样本中那么多的数据,这样的要怎么计算呢?利用训练集训练好模型之后,其实每一层的BN层都保留下了每一个batch算出来的(使用移动平均得到),利用整体训练集的无偏估计来估计测试集的。即,然后再用学习到的参数进行BN。
其他的Norm方法
不同种Norm方法之间区别如下图:
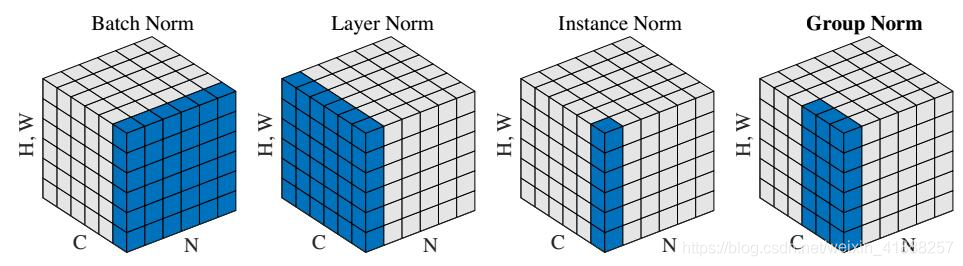
BatchNorm:batch 方向做归一化,算 N ∗ H ∗ W 的均值
LayerNorm:channel 方向做归一化,算 C ∗ H ∗ W 的均值
InstanceNorm:一个 channel 内做归一化,算 H ∗ W 的均值
GroupNorm:将 channel 方向分 group ,然后每个 group 内做归一化,算 ( C / / G ) ∗ H ∗ W 的均值
- Transformer中用BatchNorm可以吗?
LN是针对每个样本序列进行归一化,没有批量依赖,不会因为batchsize变化而变化,对一个序列的不同特征维度进行归一化。
CV使用BN是因为认为通道维度的信息对cv方面有重要意义,如果对通道维度也归一化会造成不同通道信息一定的损失。NLP认为句子长短不一,且各batch之间的信息没有什么关系,因此只考虑句子内信息的归一化。
LayerNorm是对每个样本的所有特征做归一化,BatchNorm是对一个batch样本内的每个特征做归一化。
手撕BatchNorm
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28def Batchnorm_simple_for_train(x, gamma, beta, bn_param):
"""
param:x : 输入数据,设shape(B,L)
param:gama : 缩放因子 γ
param:beta : 平移因子 β
param:bn_param : batchnorm所需要的一些参数
eps : 接近0的数,防止分母出现0
momentum : 动量参数,一般为0.9, 0.99, 0.999
running_mean :滑动平均的方式计算新的均值,训练时计算,为测试数据做准备
running_var : 滑动平均的方式计算新的方差,训练时计算,为测试数据做准备
"""
running_mean = bn_param['running_mean'] #shape = [B]
running_var = bn_param['running_var'] #shape = [B]
results = 0. # 建立一个新的变量
x_mean=x.mean(axis=0) # 计算x的均值
x_var=x.var(axis=0) # 计算方差
x_normalized=(x-x_mean)/np.sqrt(x_var+eps) # 归一化
results = gamma * x_normalized + beta # 缩放平移
running_mean = momentum * running_mean + (1 - momentum) * x_mean
running_var = momentum * running_var + (1 - momentum) * x_var
#记录新的值
bn_param['running_mean'] = running_mean
bn_param['running_var'] = running_var
return results , bn_param1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19def Batchnorm_simple_for_test(x, gamma, beta, bn_param):
"""
param:x : 输入数据,设shape(B,L)
param:gama : 缩放因子 γ
param:beta : 平移因子 β
param:bn_param : batchnorm所需要的一些参数
eps : 接近0的数,防止分母出现0
momentum : 动量参数,一般为0.9, 0.99, 0.999
running_mean :滑动平均的方式计算新的均值,训练时计算,为测试数据做准备
running_var : 滑动平均的方式计算新的方差,训练时计算,为测试数据做准备
"""
running_mean = bn_param['running_mean'] #shape = [B]
running_var = bn_param['running_var'] #shape = [B]
results = 0. # 建立一个新的变量
x_normalized=(x-running_mean )/np.sqrt(running_var +eps) # 归一化
results = gamma * x_normalized + beta # 缩放平移
return results , bn_param手撕LayerNorm
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39import torch
eps = 1e-5
class LayerNorm:
def forward(x, w, b):
# x is the input activations, of shape B,T,C
# w are the weights, of shape C
# b are the biases, of shape C
B, T, C = x.size()
# calculate the mean
mean = x.sum(-1, keepdim=True) / C # B,T,1
# calculate the variance
xshift = x - mean # B,T,C
var = (xshift**2).sum(-1, keepdim=True) / C # B,T,1
# calculate the inverse standard deviation: **0.5 is sqrt, **-0.5 is 1/sqrt
rstd = (var + eps) ** -0.5 # B,T,1
# normalize the input activations
norm = xshift * rstd # B,T,C
# scale and shift the normalized activations at the end
out = norm * w + b # B,T,C
# return the output and the cache, of variables needed later during the backward pass
cache = (x, w, mean, rstd)
return out, cache
def backward(dout, cache):
x, w, mean, rstd = cache
# recompute the norm (save memory at the cost of compute)
norm = (x - mean) * rstd
# gradients for weights, bias
db = dout.sum((0, 1))
dw = (dout * norm).sum((0, 1))
# gradients for input
dnorm = dout * w
dx = dnorm - dnorm.mean(-1, keepdim=True) - norm * (dnorm * norm).mean(-1, keepdim=True)
dx *= rstd
return dx, dw, dbPre norm和Post norm的区别
Pre-norm训练更稳定,更容易收敛。 Post-norm性能更好,但是需要warm up,且对超参数敏感,训练初期可能会有梯度消失或梯度爆炸,比较难训练。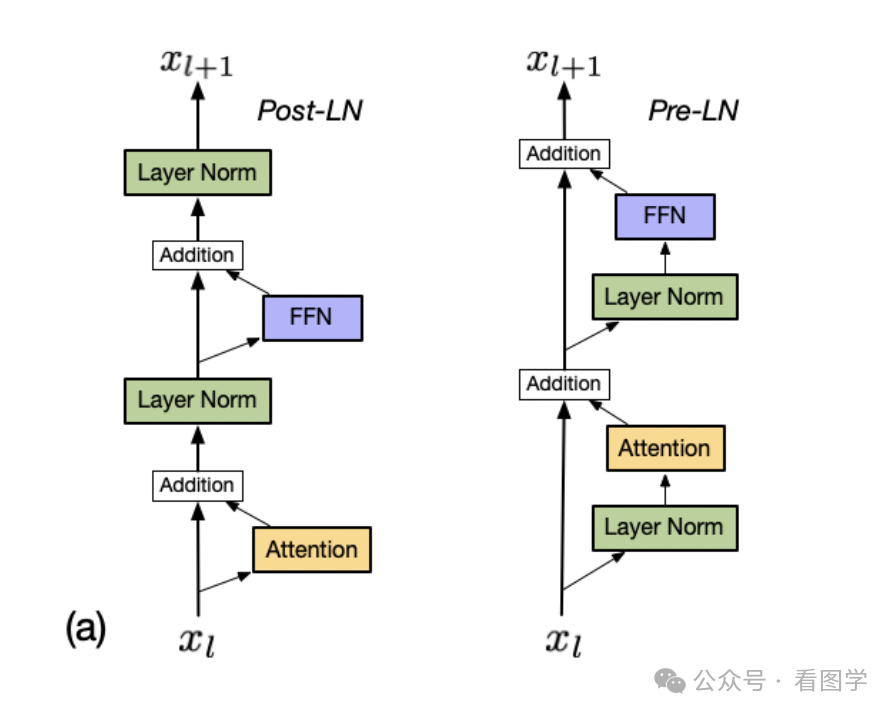
Dropout在训练和推理时的区别
训练时,随机屏蔽一部分神经元以防止过拟合;测试时,需要用完整的模型进行预测,因此禁用dropout。(可以通过model.eval())
使用dropout需要对神经元的输出重新缩放:- 假设dropout的保留率为p,在训练期间,一个神经元以概率p保留,其输出会被除以p来保持期望不变。
- 在测试期间,所有神经元保留,保持原始输出即可。
Dropout作用
是一种常用的正则化技术,训练时随机丢弃神经元,主要用于防止过拟合。
位置:Embedding之后;MHSA之后的Add&Norm之前;FFN的激活函数之后,Add&Norm之前;Decoder的最终输出层之前。
优化器
BGD优化器
BGD采用整个训练集的数据来计算loss对参数的梯度。
优点:如果是凸优化一定能取得全局最优解,如果是非凸优化可以取得局部最优解
缺点:在一次迭代中,对整个数据集计算梯度,计算起来非常慢,遇到大型数据集会非常棘手。SGD优化器
SGD 可以避免 BGD 因为大数据集而造成的冗余计算,比如 BGD 会对相似的数据进行重复计算。SGD 则是每次只选择一个样本的数据来进行更新梯度。
优点:由于一次只用一个数据,因此梯度更新很快;当然也可以进行在线学习(不用收齐所有数据)。
缺点:因为震荡,很难收敛于一个精准的极小值。MBGD优化器
小批量随机梯度下降可以看作是 SGD 和 BGD 的中间选择,每次选择数量为 n 的数据进行计算,既节约的每次更新的计算时间和成本,也减少了 SGD 的震荡,使得收敛更加快速和稳定。
缺点:选择合适的学习率仍然是一个玄学;对于非凸问题极易陷入局部最优(鞍点)。Momentum优化器
公式:,一般取0.9.
优点: 加速收敛。Adagrad优化器
公式:
优点:减少了学习率的手动调节
缺点: 学习率会收缩并变得非常小。RMSprop优化器
为了解决AdaGrad学习率急剧下降问题的。
公式:
Adam优化器
是Momentum和RMSprop的结合体,需要保存梯度和梯度平方的指数加权平均。
公式:- 由于初始时刻没有什么可平均的,因此进行偏差修正,.
- 最后更新权重。
AdamW优化器
在Adam基础上加了L2正则化项,即optimizer参数中的weight_decay项。
为什么需要Batchsize?
一次性在所有样本上训练再更新梯度资源消耗太大;一次只在一个样本上更新梯度,方差较大;使用一个batch可以更好地预估整个样本空间优化地方向。
当增大batch size时,学习率应该如何变化?
直觉上,当Batch Size增大时,每个Batch的梯度将会更准(batch size增大K倍,相当于将梯度的方差减少K倍,因此梯度更加准确),所以步子就可以迈大一点(例如将lr增加sqrt(K)倍),也就是增大学习率,以求更快达到终点,缩短训练时间。
其它
梯度消失和梯度爆炸及解决办法
梯度消失:梯度趋近于零,网络权重无法更新或更新的很微小,网络训练再久也不会有效果
原因:激活函数偏导过小,梯度连乘导致很低。
梯度爆炸:梯度呈指数级增长,变的非常大,然后导致网络权重的大幅更新,使网络变得不稳定.
原因:模型初始化权重可能很大。连乘导致爆炸。
解决方法:- 梯度截断、梯度正则;
- 使用ReLU、LeakyReLU等激活函数;
- 引入BN层;
- 使用残差结构。
什么是warm up?
模型训练开始时使用非常小的学习率,再逐渐增大。
zero shot,few shot区别
Zero-shot: 利用训练集数据训练模型,使得模型能够对测试集的对象进行分类,但是训练集类别和测试集类别之间没有交集;期间需要借助类别的描述,来建立训练集和测试集之间的联系,从而使得模型有效。
Few-shot: 旨在利用极少量的样本来训练模型,从而在新的任务中表现出良好的性能。这通常涉及到模型在预训练阶段获得大量的背景知识,然后在只提供几个新样本的情况下快速适应新任务。Pytorch中nn.eval函数和训练的区别
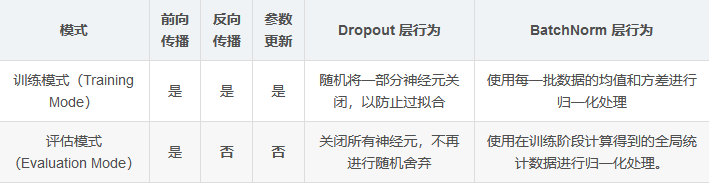
权重初始化的方法
- 常数初始化: 把权值或者偏置初始化为一个常数,例如设置为0,偏置初始化为0较为常见,权重很少会初始化为0。
- 随机分布初始化:可以使用均匀分布或高斯分布初始化(uniform)。
- xavier初始化:目的是为了使得模型各层的激活值和梯度在传播过程中的方差保持一致。在Tanh中表现好,在ReLU中表现差。
- Kaiming初始化:针对于Relu的初始化方法。本质上是高斯分布初始化,与上述高斯分布初始化有所不同,其是个满足均值为0,方差为2/n的高斯分布。