AIGC论文阅读——Diffusion及其加速采样系列

DDPM

DDPM的前向加噪过程
DDPM的反向去噪过程
DDPM的训练过程

随机采样时间步t和前向噪声epsilon，用神经网络拟合该epsilon。
DDPM的采样过程

首先从高斯分布采样初始噪声xt，然后每一步预测出epsilon来还原x_{t-1}。由于x_{t-1}是有均值方差的高斯分布，因此
预测出epsilon还原出均值后，还需要从标准正态分布中随机采样一个z来加上方差。
DDPM的生成是随机性过程吗？

是的。在DDPM的反向过程中，每一步都会采样一个噪声，然后利用这个噪声和前一步的输出来生成下一步的图像。这个过程是随机的，因为每一步都会引入新的随机性。

DDIM

DDIM的采样过程

DDIM的采样过程是非马尔可夫的，且由于eta设置为0，每一步去噪无需重采样高斯噪声（除了第一步采样x_t），因此采样过程是一个确定性过程。

单独DIIM并没有加速，加速使用respacing（按照一定间隔减小采样步数）。只不过respacing对DDPM使用会大幅降低生成效果，但是DDIM不会。所以DDIM+respacing又快又好。
DDIM的Inversion

DDIM除了可以确定性去噪外，还可以确定性加噪，从而实现Image editing。
DDPM与DDIM的区别

DDPM：固定sample方差为beta或者\hat{beta}。
DDIM：固定方差为0，配合respacing实现加速。

V-Prediction

V-prediction的原理

DDPM中，加噪过程公式为
$x_t=\sqrt{\overline{\alpha_t}}x_0+\sqrt{1-\overline{\alpha_t}}\epsilon$ 。
在V-prediction的表示中，该公式被写成
$x_t=\alpha_tx+\sigma_t\epsilon$ 。
这里的 $\alpha_t$ 相当于DDPM中的 $\sqrt{\overline{\alpha_t}}$ ，x相对于DDPM中的 $x_0$ ， $\sigma_t$ 相当于DDPM中的 $\sqrt{1-\overline{\alpha_t}}$ 。

易知在单位圆上。速度v定义为这条半径的切线方向，也就是其导数：
$v=\alpha_t\epsilon-\sigma_tx$ 。
对v的公式和 $x_t$ 的公式联立，利用 $\alpha_t^2+\sigma_t^2=1$ ，可得到预测的原图的表达式:
$\hat{x}=\alpha_tz_t-\sigma_t\hat{v_\theta}(z_t)$ ，
其中 $\hat{x}$ 为预测的原图， $z_t$ 为当前时间步的噪声， $\alpha_t和\sigma_t$ 参见上面定义， $\hat{v_\theta}$ 为去噪网络。

在训练阶段，依然使用DDPM给原图加噪，不过模型预测目标是v，并用公式计算出的结果监督。

在推理阶段，模型预测出速度v，可以用上边的 $\hat{x}$ 计算出预测的原图，和xt加权求出xt-1再继续去噪。

从v的表达式来看，它是原图x0和噪声的加权求和，因此可以把对速度的预测看作介于直接预测原图和直接预测噪声中间的一个预测目标。

NCSN(Generative Modeling by Estimating Gradients of the Data Distribution)

更详细的请阅读原论文及Yang Song的博客

NCSN的核心思想
1. 使用神经网络去预测数据分布的score（对数概率密度的梯度），也即Score matching。
2. 使用退火朗之万运动学(Annealed Langevin dynamics)去还原原始数据分布。
Score matching是什么？

对于一些来自未知数据分布的独立同分布样本，定义其数据分布为Pdata。我们称其对数概率密度的梯度为Score。使用一个神经网络Score network来拟合该数据分布的score，而不是像GAN一样直接拟合数据分布。Score matching的目标就是最小化 $E_{pdata}[\|s_\theta(x)-\nabla_x log_{pdata}(x)\|_2^2]$ 。
如何使用朗之万动力学进行采样？

朗之万动力学可以通过使用Score function来从概率密度函数中采样。给定一个固定的step size $\epsilon\gt 0$ ，一个初始值 $\tilde{x}_0 \backsim \pi(x)$ ，其中 $\pi(x)$ 为一个先验分布。朗之万通过递归地计算下式：
$\tilde{x}_t = \tilde{x}_{t-1}+\frac{\epsilon}{2}\nabla_x logp(\tilde{x}_{t-1})+\sqrt{\epsilon} z_t,z_t\backsim N(0,I)$
当 $\epsilon \rarr 0,T\rarr \infty$ ，则相当于从原分布中采样。

因此，要从原始分布pdata中采样，先训练score network来估计score，再使用朗之万动力学进行采样。
Score-based generative modeling中存在的挑战
1. 流形假说：数据通常在低维流形空间上。但是score matching的目标当数据分布在整个空间上时会更consistent。例如直接在CIFAR-10上训练score matching会不收敛，但如果使用高斯噪声去perturb原始数据，则更有利于score matching学习（因为强行将数据分布的support扩展到整个空间）。
2. Scrore estimation对低数据密度区域的估计不准确，同时也会使朗之万动力学收敛缓慢。
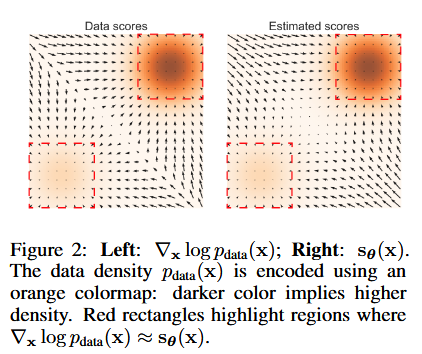
NCSN(Noise Conditioned Score Networks)提出的解决方案
针对上面的问题，提出两个策略：（1）用不同level的noise去扰动数据。（2）训练一个使用noise level作为条件的score estimator。
- 训练目标：
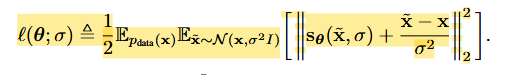
- 采样过程，使用退火朗之万动力学：