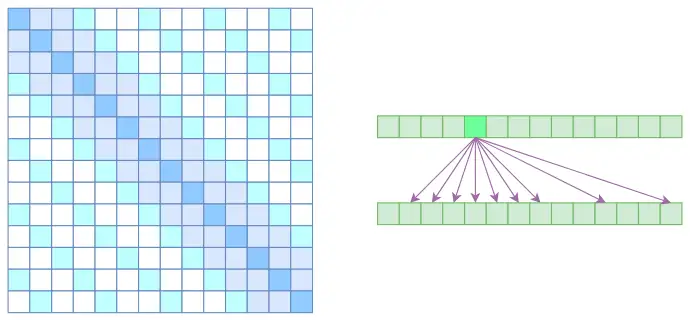
Scaled dot-product attention的时间和空间复杂度都是O(n^2)的,当n较大时,会是很大的占用。
Sparse attention
将空洞注意力与局部注意力相结合,使得既可以学到局部的特性,又可以学到远程稀疏的相关性。使得大部分元素为0,时间与空间复杂度下降为O(kn)。但是其是对标准attention的近似。
Flash attention
Flash Attention v1原理
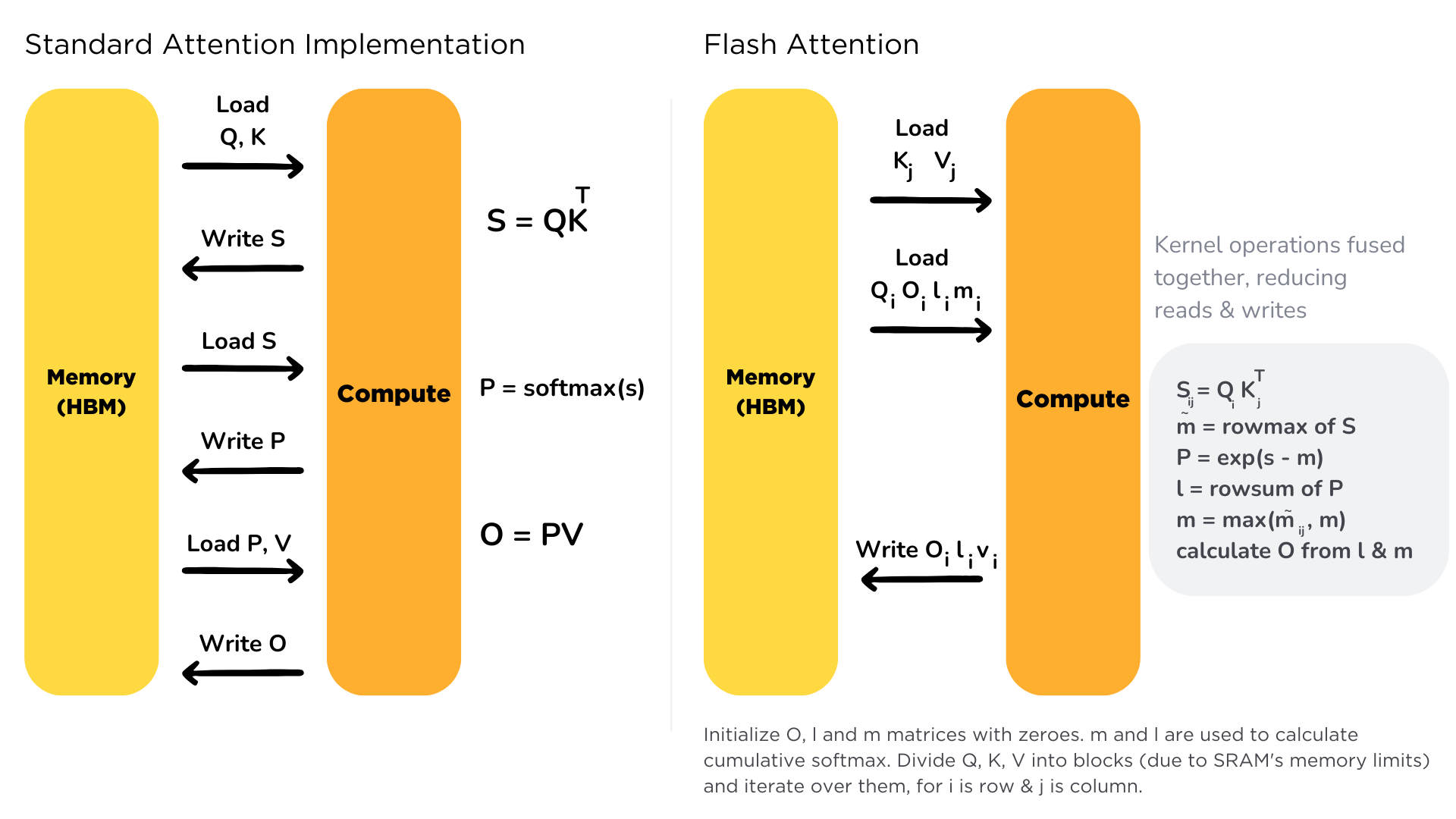
原理:减小MAC:使用Tiling技巧将Q,K,V分块后存入SRAM中,使用增量更新的技巧来计算Softmax值以及加权后的V值,再存回HBM,极大地减小了与HBM的IO开销。
大部分的Efficient transformer的目标都是减少FLOPs。Flash Attention的目标是降低MAC(Memory Access cost),代价是增加了FLOPs. Flash attention是一种精准的优化策略,没有近似损失。
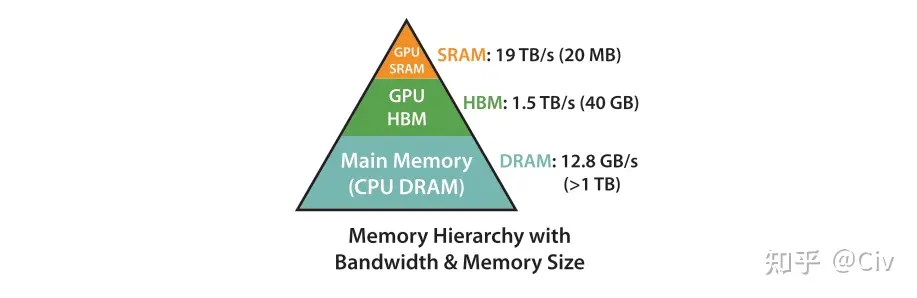
GPU的存储由SRAM和HBM组成。SRAM的读写速度远大于HBM,但其存储空间远小于HBM。
为了减少对HBM的读写,Flash attention将参与计算的矩阵进行分块送进SRAM,来提高整体读写速度。对于Flash attention来说,矩阵分块计算不是难事,重要的是Softmax值的计算——这里采用的是增量计算,具体请参考知乎文章及下列伪代码:
Flash Attention v1与Transformer的MAC分析。
标准Transformer的MAC次数:
第一行,读Q,K的MAC次数位2Nd,写S的MAC次数为N^2。
第二行,读S的MAC次数为N^2,写P的MAC次数为N^2。
第三行,读P的MAC次数为N^2,读V的MAC次数为Nd,写O的MAC次数为Nd。
上述总MAC开销为4Nd+4N^2,复杂度为O(Nd+N^2)。
Flash attention v1的MAC开销:
上述伪代码中,一次完整的内循环需要读取完整的Q,MAC开销为Nd。
外循环的次数为T_c次,即T_c = 4dN/M,可知开销为O(N^2 * d^2 * M^-1)。因为M(100KB)通常远远大于d(几K),所以Flash attention的MAC远小于标准attention。
Flash attention能够将标准的self-attention的计算速度提升2至4倍。
代码见此知乎文章
Flash attention如何减少显存?
与Gradient checkpointing类似,只保存部分中间激活值,在反向传播时重新计算。用时间换空间。
KV cache
KV cache的适用范围。
适用于Decoder-only的LLM的推理过程(每一个token的输出只依赖于它自己以及之前的输出);并且每次新添加token作为输入后,原token的输入输出不会变。(一旦输入预处理层不满足KVCache的条件,后续transformer层的输入(即预处理层的输出)就发生了改变,也将不再适用于KVCache。)
KV cache的工作原理。
思想:以空间换时间,减少重复计算。将FLOPs从O(n2)降低到O(n)。
Decoder-only的attention,每次附加上新的token后,下一个token的生成只依赖于当前token的query以及所有token的key和value。因此在推理的自回归过程中,我们只需要计算当前token的qkv,然后将它的kv与之前的kv进行concat后计算attention score即可,其他部分是不变的。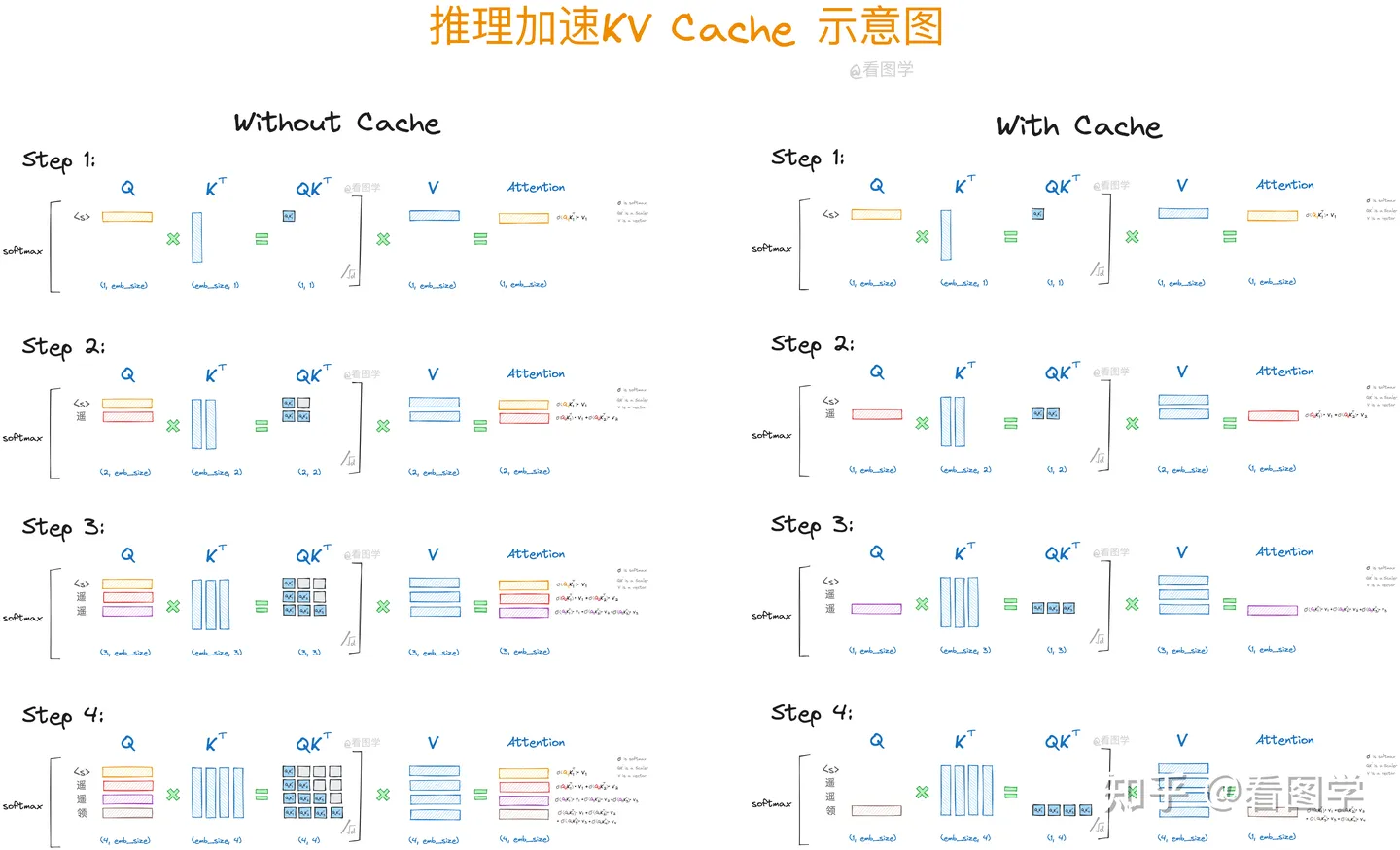
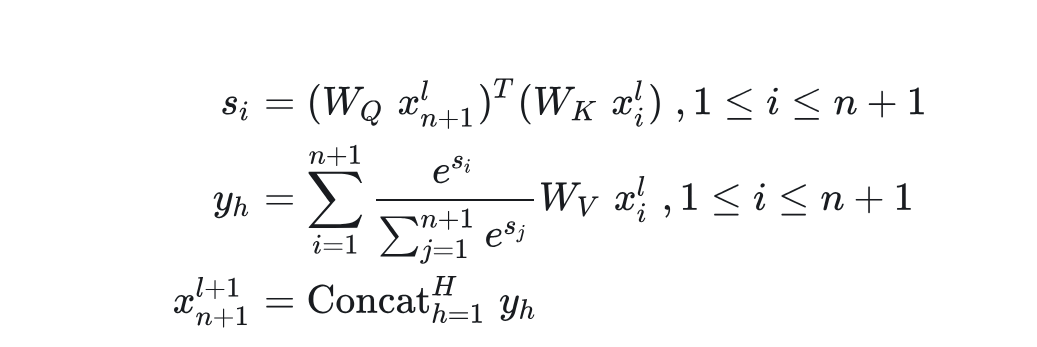
KV cache占用内存大小
假设Transformer有n_layers层,每个多头注意力层有n_heads个头,维度为d_head,需要为K和V都缓存一份;最大上下文长度为n_context,精度为n_bytes,推理的批量为batch_size。
则KV cache需要的内存大小为2 * n_layers * n_heads * d_head *n_context * n_bytes * batch_size。
为什么是KV cache而不是Q cache?
因为下一个token只取决于最新token的Q和所有token的KV(因果性),每一次用的Q都是最新的。
Multi Query Attention(MQA)与Group Query Attention(GQA)
MQA的动机及原理
动机:KV cache中对于多头,每个头都会有一个K,V矩阵。因此KV cache较大。
原理:MQA让所有头之间共享同一份K和V矩阵,从而大大减少KV参数量和cache量。这样在decoder上推理时,可以大大减少KV cache大小。能提高 30%-40% 的吞吐。
GQA的原理
将query分为N组,每个组共享一个K和V矩阵。
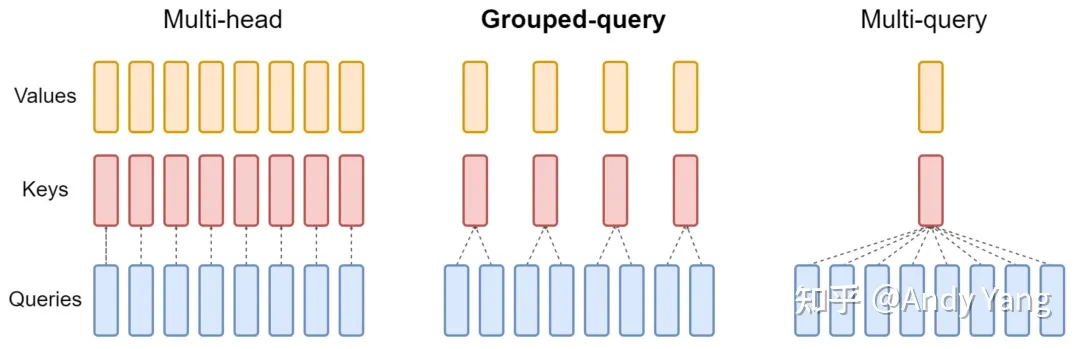
MQA和GQA的共同原理
降低了从内存中读取的数据量,所以也就减少了计算单元等待时间,提高了计算利用率;
KV cache 变小了 head_num 倍,也就是显存中需要保存的 tensor 变小了,空出来空间就可以加大 batch size,从而又能提高利用率。
手撕MQA和GQA
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66class GroupQueryAttention(nn.Module):
def __init__(self, heads, d_model,group_num):
super().__init__()
self.d_model = d_model
self.d_k = d_model // heads # 每个“头”对应的维度
self.h = heads # “头”的数量
self.group_num = group_num # 分组数,当group_num=1时,为MQA
# 初始化线性层,用于生成Q,K,V
self.q_linear = nn.Linear(d_model, d_model)
self.k_linear = nn.Linear(d_model, self.d_k*group_num)
self.v_linear = nn.Linear(d_model, self.d_k*group_num)
# 输出线性层
self.out = nn.Linear(d_model, d_model)
def attention(self, q, k, v, mask=None):
# q,k,v [...,d]
# 计算点积,并通过 sqrt(d_k) 进行缩放
scores = torch.matmul(q, k.transpose(-2, -1)) / math.sqrt(self.d_k)
# 如果有 mask,应用于 scores
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9)
# 对 scores 应用 softmax
scores = F.softmax(scores, dim=-1)
# 获取输出
output = torch.matmul(scores, v)
return output
def split_head(self,x,group_num=None):
batch_size, seq_len = x.size()[:2] # 获取批量大小和序列长度
if group_num is None:
return x.reshape(batch_size, -1, self.num_heads, self.head_dim).transpose(1, 2)
else:
# 将 hidden_size 分割为 group_num 和 head_dim
x = x.reshape(batch_size, -1, group_num, self.head_dim).transpose(1, 2)
# 再将其手动 expand 到相同大小
x = x[:, :, None, :, :].expand(batch_size, group_num, self.num_heads // group_num, seq_len, self.head_dim).reshape(batch_size, self.num_heads, seq_len, self.head_dim)
return x # 形状: (batch_size, num_heads, seq_len, head_dim)
def forward(self, q, k, v, mask=None):
# q,k,v:[B,T,d]
batch_size = q.size(0)
# 对 q,k,v 进行线性变换
q = self.q_linear(q) # [B,T,d_model]
k = self.k_linear(k) # [B,T,d_k*group_num]
v = self.v_linear(v) # [B,T,d_k*group_num]
# 分组
q = self.split_head(q) # [B,num_heads,T,head_dim]
k = self.split_head(k,group_num=self.group_num) # [B,num_heads,T,head_dim]
v = self.split_head(v,group_num=self.group_num) # [B,num_heads,T,head_dim]
# 进行多头注意力计算
scores = self.attention(q, k, v, mask)
# 将多个头的输出拼接回单个张量
concat = scores.transpose(1, 2).contiguous().view(batch_size, -1, self.d_model)
# 通过输出线性层
output = self.out(concat)
return output